NeRF Learning
2025-11-14, updated on 2025-11-27
Introduction
笔者将在这篇博客中记录学习NeRF以及NeRF-SR等相关知识(持续更新)的一些笔记,欢迎一起讨论~
0.NeRF Basic
NeRF的全称是Neural Radiance Field(神经辐射场),是一种基于神经网络的渲染方法,其主要目标任务是“新视角合成”。 它的核心思想大致可概述为用一个MLP(全连层而非卷积,加上激活层)神经网络去隐式地学习一个静态3D场景,实现复杂场景的任意新视角合成(渲染)。 NeRF使用多视角的数据进行训练,空间中目标位置具有更高的密度和更准确的颜色,促使神经网络预测一个连续性更好的场景模型。 以任意的相机位置+朝向作为输入,经过训练好的神经网络进行体渲染(Volume Rendering),就可以得到任意视角的图片。
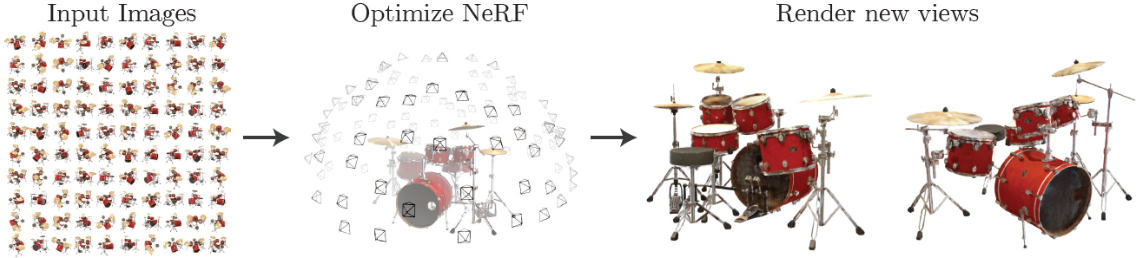
0.0 图形学基础
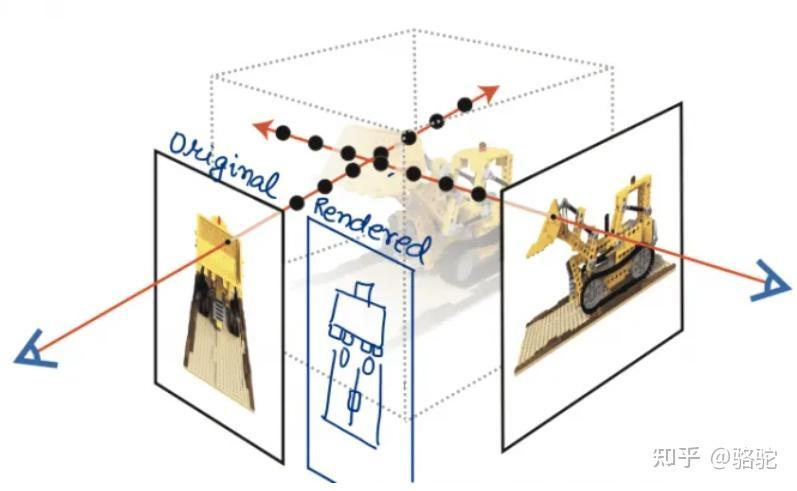
给出一个理解角度:NeRF 模型的输出可以看作某条 Ray 上面的一个点, 对这条 Ray 的所有的点做积分, 可以得到相应 Pixel 的 RGB 值。
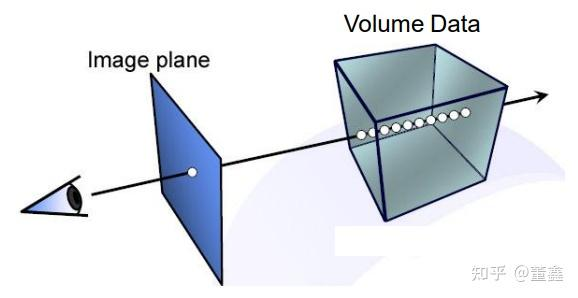 具体言之,先用 NeRF 找到箭头与 Volume Data (就是 3D 物体) 的若干个交点, 然后对这些交点做积分
而这个ray是什么呢?实际上就是我们的“眼睛”或者说相机“发出”(实际是接受)的光
具体言之,先用 NeRF 找到箭头与 Volume Data (就是 3D 物体) 的若干个交点, 然后对这些交点做积分
而这个ray是什么呢?实际上就是我们的“眼睛”或者说相机“发出”(实际是接受)的光
那么我们怎么描述这个射线呢?
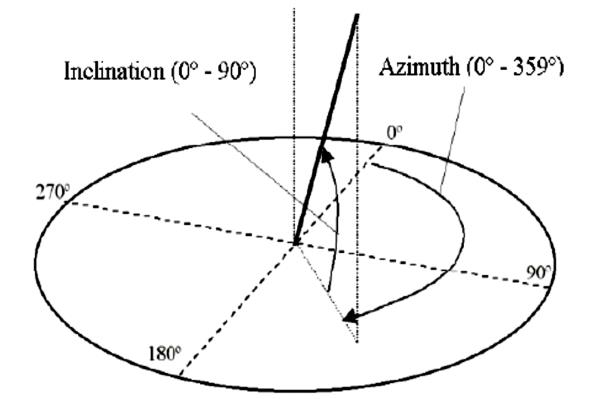
除了相机/眼睛的三维位置外,我们还需要两个量来描述相机的视角,即角度:inclination 倾角 和 azimuth 方位角
而这每一条Ray都对应我们最后要渲染出来的一个像素,于是自然有: 如果你最终要生成的图片大小是 $H \times W$,, 那么就有 $H \times W$ 条 Ray 从 相机 (你的眼睛) 射出。
下面对每一条ray进行描述: 一条 Ray 可以用它的起点 $ v_0 $和终点 $ v_d$ (这个不是真正的终点, 因为理论上 Ray 可以无限延伸) 描述
起点肯定就是相机 (你的眼睛), 终点就是一个能够指示方向的单位向量
于是ray上任意一点就可表示为 \(P = v_0 + t * v_d\)
其中t是任意的实数,采样点也就是选不同的t
那么渲染具体是怎么实现?
我们尝试看一看理解NeRF的数据集组织: 首先, 我们引入几个概念
全局坐标参考系 (World Coordinate Frame)
相机坐标参考系 (Camera Coordinate Frame)
坐标变换 (Coordinate Transformation)
投影变换 (Projection Transformation)
全局一般就是物理世界的尺度,一般不会变 相机坐标参考系, 是针对相机的某个位置而言的. 对于同一个 3D 物体,可以从不同的角度去拍它, 那么自然一旦相机的位置 (pose) 发生改变, 相机坐标参考系也会变化
那么同一个点在不同的坐标参考系下肯定是表示不同,我们需要通过“坐标变换”来构建一个映射关系 转换可以写成一个数学公式: \(X_c = R \times (X_w - C_w)\)
R是一个3x3的旋转矩阵, $C_w$是相机在全局坐标系中的位置, $X_w$是全局坐标系下的点

那么我们肯定就是要在数据集里面刻画好这个四维的转换矩阵:

我们如果称变换前的坐标系叫做 “旧坐标系”, 变换后的坐标系叫做 “新坐标系”
对于这个新的四维矩阵,我们还有一个性质必须要说明:
 这里面的前三列, 分别表示 新坐标系 (红的是 x 轴, 紫的是 y 轴, 黄的是 z 轴) 在旧坐标系中的方向, 最后一列 (绿色) 是 新坐标系原点在旧坐标系中的位置.
这里面的前三列, 分别表示 新坐标系 (红的是 x 轴, 紫的是 y 轴, 黄的是 z 轴) 在旧坐标系中的方向, 最后一列 (绿色) 是 新坐标系原点在旧坐标系中的位置.
我们先画个示意图简化讨论这个问题: P(C)是3D物体上的某个点,A是相机的位置,C’是我们希望刻画的2维的image plane上的点
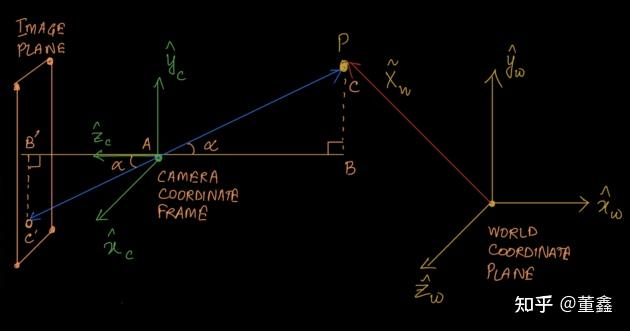
那么我们想要刻画的就是C’(xi,yi)
我们有B’A = focal length,记为f 假设相机参考系: P:(X,Y,Z)
那么C’的坐标可以表示为:
\[C'_x = (X/Z)\times f\] \[C'_y = (Y/Z) \times f\]if not os.path.exists('tiny_nerf_data.npz'):
!wget http://cseweb.ucsd.edu/~viscomp/projects/LF/papers/ECCV20/nerf/tiny_nerf_data.npz
data = np.load('tiny_nerf_data.npz')
images = data['images']
poses = data['poses']
focal = data['focal']
这里可以看到实际代码中数据集的组织 images, 就是从各个角度拍的 2D 图片 poses, 就是代表相机的位置及角度,具体说就是我们刚才说的这个四维变换矩阵 focal, 就是前面讲过的 focal length f
那么再由我们刚才提到的特殊性质,我们自然有最后一列就是 相机位置 (在全局坐标参考系中). 然后第三列就是 相机的角度 (因为第三列是相机坐标系的 z 轴, 而相机都是沿着 z 轴拍摄的)
可视化出相机方向大概就这样:
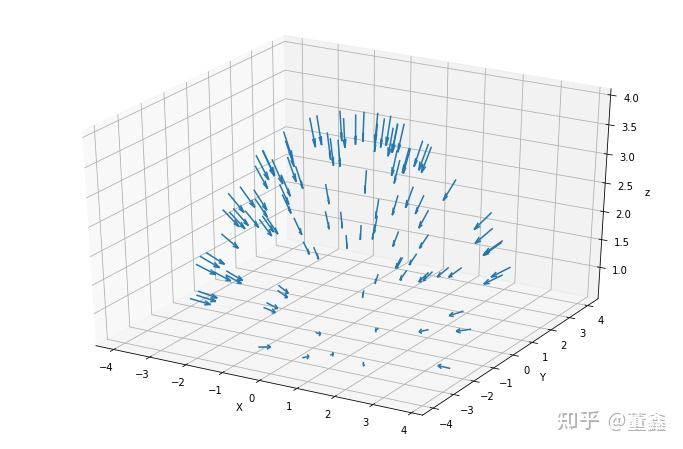
最后有了以上的推导,我们就可以刻画出Ray了
我们首先引入第三个参考系:
图片坐标参考系 (Image Plane Coordinate Frame)
首先, 这个图片坐标参考系是二维的, [注意 Image Plane 的左上角的像素位置设为 (0, 0)]
其次, 他其实就是 相机坐标参考系 的退化版, 相当于 相机坐标参考系 去掉了 z 轴.
我们知道, 画一个 Ray 其实很简单, 那就是
1) 找到一个 Image Plane 上的像素点; 2) 找到 相机 (你的眼睛) 原点; 3) 把这两个点连线.
假设某个像素点的位置是 (i, j) , 那么他在 相机坐标参考系 中的位置是 (i - width0.5, j - height0.5) [因为相机坐标参考系的 z 轴正好穿过 Image Plane 的中点]
那么这个 Ray 的方向就是:
\[((i - width*0.5) / \text{focal_length}, (j - height*0.5) / \text{focal_length}, -1)\]也是上面图6的α
注意到, 我们刚刚求出来的方向, 是在相机坐标参考系求的, 我们还要把它转到全局坐标参考系中, 那就是直接 ×转换矩阵
而Ray的原点实际上我们也讨论过了,就是转换矩阵的最后一列前三行
directions = torch.stack([(i - width * .5) / focal_length,
-(j - height * .5) / focal_length,
-torch.ones_like(i)
], dim=-1) # 在相机坐标参考系中的方向
rays_d = torch.sum(directions[..., None, :] * c2w[:3, :3], dim=-1) # 在全局坐标参考系中的方向
rays_o = c2w[:3, -1].expand(rays_d.shape) # 在全局坐标参考系 中的 相机/Ray 原点
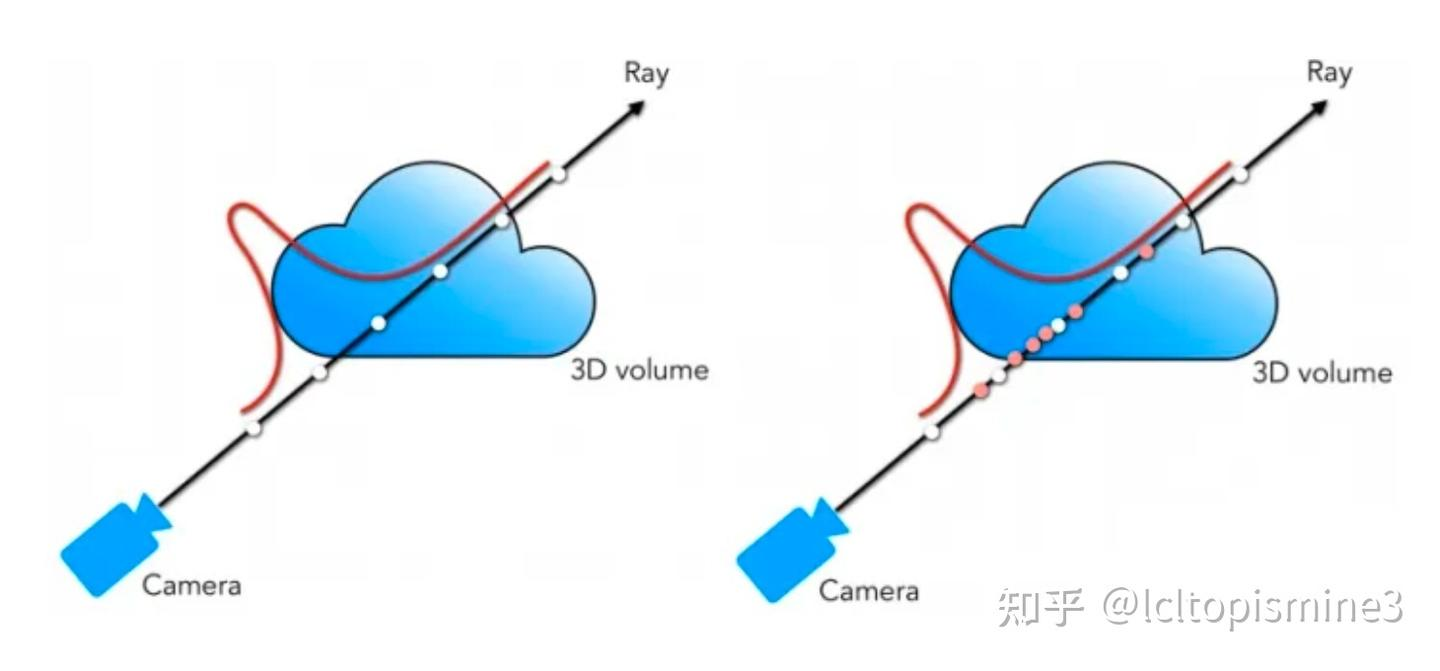
有了Ray,下一步就是采样上面的点: NeRF 的关键在于找到 Ray 和 Volume Data (就是 3D 物体) 之间的交点, 然后对这些交点的(R,G,B,$\sigma$)做积分. 这里的 $\sigma$ 就是这个点的”透明度”)做积分.
没有3D模型的话我们不能直接找到这些点 NeRF 采用的方式是 “试”
先随机的沿着当前 Ray 采样一堆点, 然后我带入到 NeRF 中, 如果某个点的$\alpha = 0 $, 那么说明这个点不是交点, 反之就是.
这里感觉还是不太清晰(,为啥α是0啊,欢迎comment
\(P = v_0 + l * v_d\) 所以我们沿着Ray找点无非是试不同的l
采样方法: 比如均匀采样 (Stratified Sampling), 就是均匀的试不同的l 另外也有一些方法, 比如在均匀采样的基础上加上一些 perturbation(扰动).
另外, 因为我们肯定是只能采样有限个点, 那么一般会确定一个最大和最小的 near < l < far
像原 NeRF 论文中, near = 2, far = 6.
0.1 原始NeRF 整体架构和做法
有了图形学原理,我们就知道了NeRF是怎么采样和利用、组织数据的,下面看下NeRF的架构和设计
这篇2020的工作实际上在网络结构上非常简单粗暴,就是全连接层
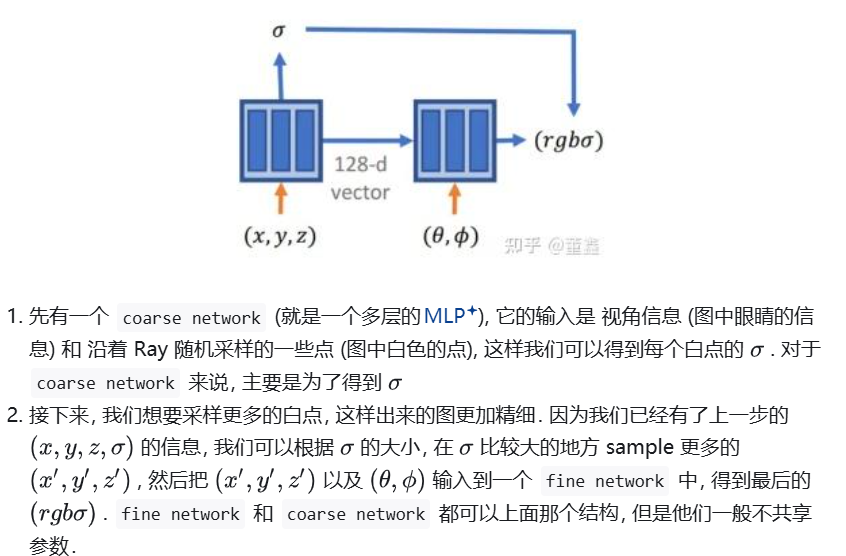
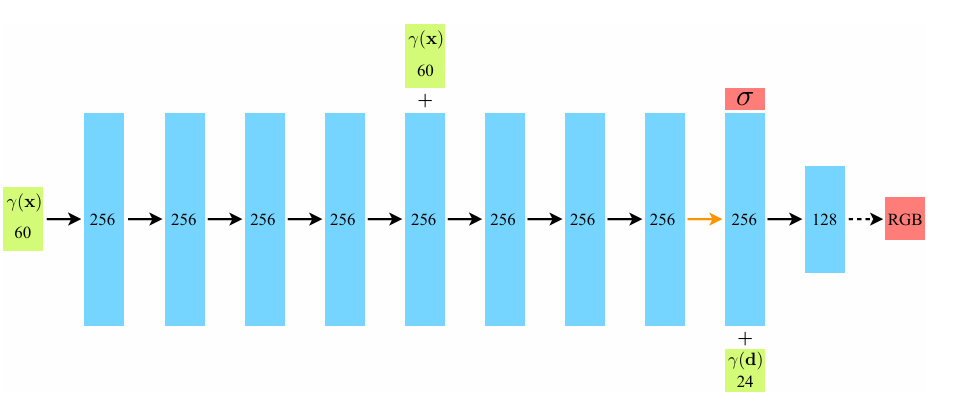
1 NeRF
这部分可能不会写的特别完全(NeRF后续的一些变种之类),可能还是先focus2020年这一篇工作中提到的一些技术和主观结果,毕竟精力有限qwq)
在开始之前,回到原论文,总结一下我们刚才得到了什么:
 也即我们可以看到原论文的理论是用一个Ray上的积分式来计算最后渲染出来的位置颜色到底应该是什么,本质是“把射线穿过的所有3D点的颜色,按‘到达该点的概率(( T(t) ))’和‘该点的贡献权重(( \sigma ))’加权后,累加得到最终2D像素的颜色”
也即我们可以看到原论文的理论是用一个Ray上的积分式来计算最后渲染出来的位置颜色到底应该是什么,本质是“把射线穿过的所有3D点的颜色,按‘到达该点的概率(( T(t) ))’和‘该点的贡献权重(( \sigma ))’加权后,累加得到最终2D像素的颜色”
(当然回看原论文中的推导,这些符号还是有点恶心qaq(主要是很难找一个合适的翻译和对应))
| 符号 | 名称/含义 | 解释 |
|---|---|---|
| ( t_n ) | 就是积分开始的地方,最接近照相机的位置 | 射线进入场景的起始位置对应的参数(比( t_n )小的区域不在场景内) |
| ( t_f ) | 积分终点 | 射线离开场景的终止位置对应的参数(比( t_f )大的区域不在场景内) |
| ( t ) | 被积的量,射线的参数变量 | 描述射线沿方向延伸的距离,对应空间位置( \mathbf{r}(t) = \mathbf{o} + t\mathbf{d} )(( \mathbf{o} )是相机位置,( \mathbf{d} )是射线方向) |
| ( T(t) ) | 透射率(Transmittance) | 射线从近裁剪面( t_n )传播到位置( t )时,未被任何粒子阻挡的概率(取值0~1) |
| ( \sigma(\mathbf{r}(t)) ) | 体积密度(Volume Density) | 空间位置( \mathbf{r}(t) )处的“不透明度程度”:射线在该点被粒子阻挡的微分概率(( \sigma )越大,该位置越“实”) |
| ( \mathbf{c}(\mathbf{r}(t), \mathbf{d}) ) | 方向辐射亮度(Directional Radiance,就是某个点的RGB) | 空间位置( \mathbf{r}(t) )处、沿射线方向( \mathbf{d} )(相机视角)呈现的颜色值(RGB三通道向量) |
我们主要再来解释一下T(x)吧,这个被一些人翻译为“透射率”,是用我们之前提到的透明度$\sigma$来计算的:

(其实从上面每个量的含义大致能猜到T(t)会是用 $\sigma$ 积出来)
当然上面只是理论值,是理想情况下的,实际中不可能做到连续的采样,而是使用离散的采样点:
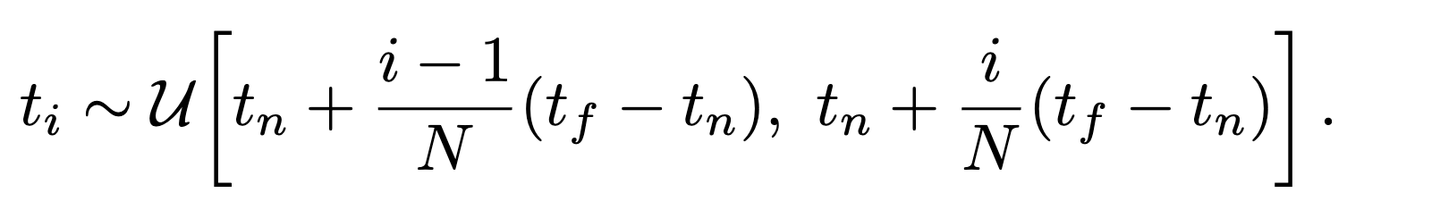
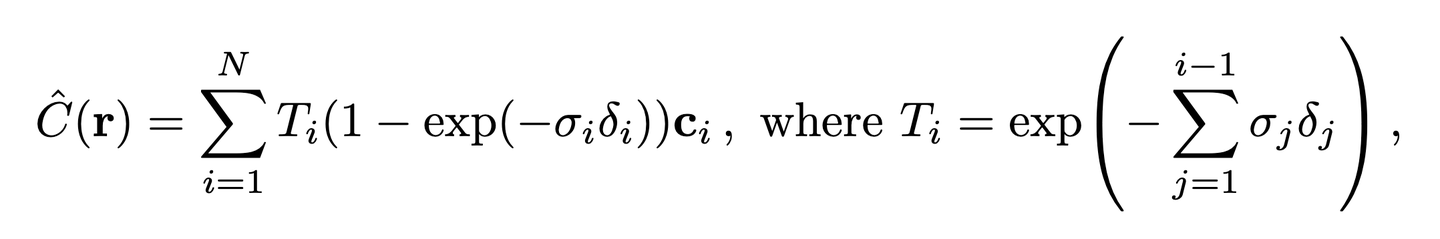
其中 $\delta_j = t_{i+1} - t_i$ 即采样间隔。$\exp(-\sigma_i \delta_i)$ 表示在第 $i$ 个点没有碰上粒子的概率,所以 $(1 - \exp(-\sigma_i \delta_i))$ 表示在该处碰到粒子的概率。
1.1 NeRF的一些trick
1.1.1 Positional encoding
作者实验发现,
- MLP倾向于学习低频信息,而导致在渲染表示颜色和几何图形的高频变化方面表现得很差。
- 在将输入传递到网络之前,使用高频函数将输入映射到更高维空间,可以更好地拟合包含高频变化的数据。
所以引入“位置编码”,它的核心就是“高频特征的放大器”
公式是: [ \gamma(p) = \left( \sin(2^0 \pi p), \cos(2^0 \pi p), \dots, \sin(2^{L-1} \pi p), \cos(2^{L-1} \pi p) \right) ]
- ( p ):
表示要编码的原始输入变量——在NeRF里,( p )有两种:
- 一种是3D空间位置 ( \mathbf{x} = (x,y,z) )(描述场景里的某个点);
- 另一种是观察方向 ( \mathbf{d} = (d_x,d_y,d_z) )(描述相机看这个点的角度)。
-
( 2^k \pi p )(( k从0到L-1 )): 这是不同频率的“震荡因子”——( 2^k )是“频率缩放”:( k=0 )对应最低频(变化最慢) 用不同频率的函数,是为了让编码能覆盖“从低频到高频”的所有细节。
- ( \sin(\dots)、\cos(\dots) ):周期性的高频函数,能把原始输入的细微差异,转化为高维空间里的“独特特征”(比如两个相邻的3D点,编码后会有明显的高维向量差异)。
实际用法
- 对3D位置 ( \mathbf{x} ):取 ( L=10 ) 3D位置是3维向量,每个维度要做 ( L=10 ) 组“sin+cos”编码,所以编码后维度是:( 3 \times 2 \times 10 = 60 ) 维。
- 对观察方向 ( \mathbf{d} ):取 ( L=4 ) 观察方向是3维单位向量,编码后维度是:( 3 \times 2 \times 4 = 24 ) 维。
“先编码,再进MLP”: [ F_\Theta = F’\Theta \circ \gamma ] 意思是:先把原始的3D位置+观察方向,用 ( \gamma )(位置编码)转换成高维向量(60+24=84维),再输入到MLP(( F’\Theta ))里,让MLP能学到高频细节(比如纹理、边缘)。
用不同频率的正余弦函数,把低维的位置/方向,映射成高维向量
1.1.2 分层采样
分层采样的核心是“分区间+区间内随机”,步骤如下:
- 划分区间:把射线的t范围(从近裁剪面( t_n )到远裁剪面( t_f )),均匀分成( N )个等宽的小区间: 第( i )个区间的范围是:( \left[ t_n + \frac{i-1}{N}(t_f - t_n),\ t_n + \frac{i}{N}(t_f - t_n) \right] )
- 区间内随机采样:在每个小区间里,随机选一个点作为采样点( t_i ),公式是: [ t_i \sim \mathcal{U}\left[ t_n + \frac{i-1}{N}(t_f - t_n),\ t_n + \frac{i}{N}(t_f - t_n) \right] ] (( \mathcal{U} )表示“均匀随机”,意思是这个区间里每个位置被选中的概率一样) 经过以上,我们能得到一个粗的采样; 之后我们权重归一化后用“逆变换”进行第二组采样,得到fine(相当于我们希望在“重要‘位置多采
先coarse,再fine:在第一组和第二组采样的并集处评估我们的“精细”网络
当然,粗采样也作为输出图片
分层采样的优势:
- 覆盖性好:把射线分成N个区间,每个区间都有一个样本,不会漏掉某段区域的场景信息;
- 避免离散偏差:区间内随机采样,让MLP在优化时能接触到连续的空间位置(不是固定点),从而学会表示连续的场景(比如精细纹理);
- 效率高:每个区间只采1个点,N不用特别大就能兼顾精度和速度。
1.1.3 loss

1.2 NeRF的一些results

2 NeRF-SR
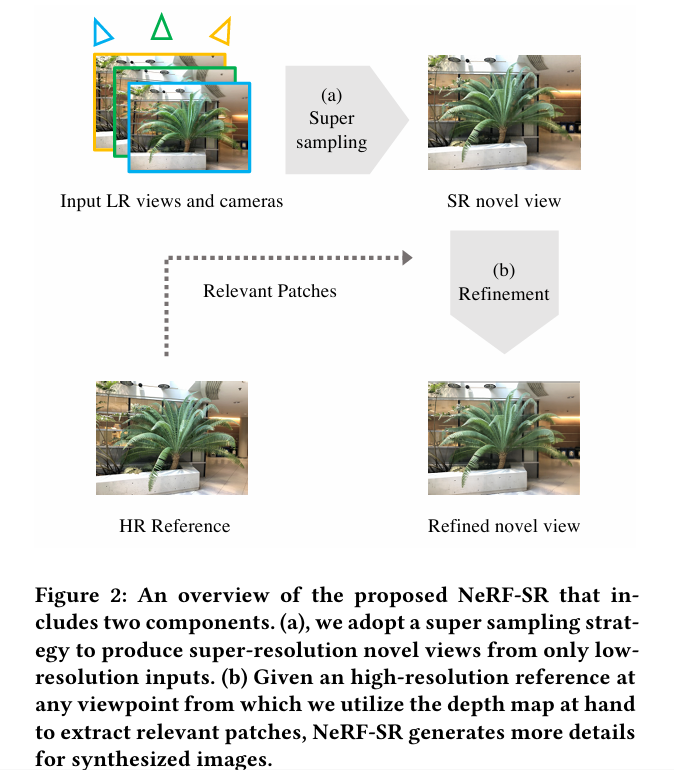
2.1 Super Sampling
一般的NeRF都达不到Nyquist sampling rate(就是观察视角的有限决定了其无法满足监督的要求),只能通过插值的方法来补充。
作者的超采样分为两种含义,一个是每个像素的超采样,即使用亚像素的方式将每个像素所占有的面积进行分割,分别进行color的预测,属于scale上的扩展;二是不同角度的扩展. (tips:实际上,用Blender渲染就不会出现这个问题。渲染可以提供所有视角所有scale的监督图像。)
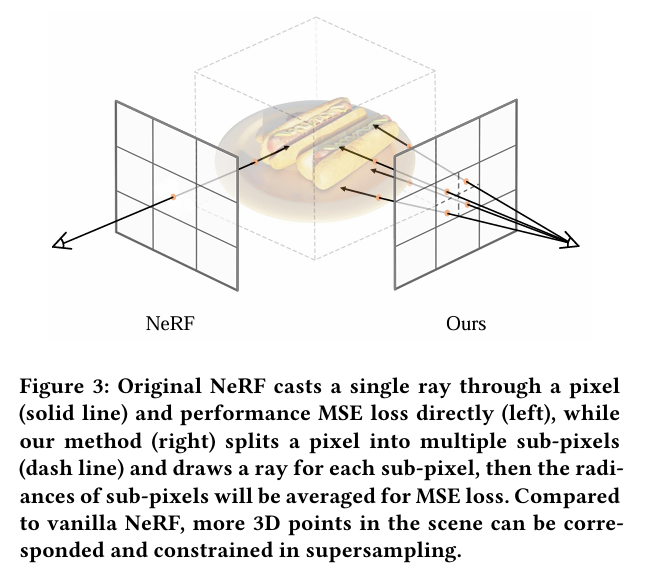 超采样策略将一个像素(实线)分割为多个子像素(虚线),并为每个子像素绘制一条射线。因此,与普通的NeRF相比,场景中更多的3D点可以被对应和约束。
超采样策略将一个像素(实线)分割为多个子像素(虚线),并为每个子像素绘制一条射线。因此,与普通的NeRF相比,场景中更多的3D点可以被对应和约束。
超采样充分利用了NeRF引入的交叉视图一致性(cross-view consistency)到亚像素级(sub-pixel level),即一个位置可以通过多个视点进行对应。虽然NeRF对每个像素只拍摄一条射线,并优化了该射线上的点,但超采样限制了三维空间中更多的位置,更好地利用了输入图像中的多视图信息。换句话说,超级采样直接在训练时优化了一个更密集的辐射场。
优化后要对应调整监督的MSE-loss,适配监督图像的大小
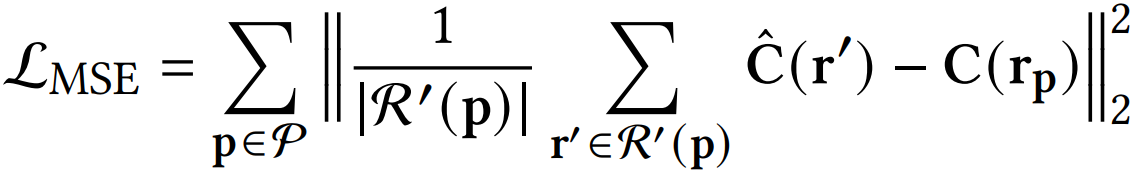
关于这部分看到的一个锐评(
感觉有些多此一举,大可以直接用光线的数量多少来做,何必非得在物理上划分成子块。或者我一开始就用子块大小的规模作为我的像素块就得了
2.2 Patch-based Refinement
当一个场景的图像没有足够的亚像素对应时,超采样的结果无法找到足够的细节来进行高分辨率的合成。因此,作者提出了Patch-Based Refinement 网络来恢复高频细节,旨在将参考图像的细节融合到NeRF合成的模型-图像中。基本就是在渲染合成的图像的基础上再加一个Unet网络,将渲染图像的patch作为输入,以对应的参考图像的patch作为监督。
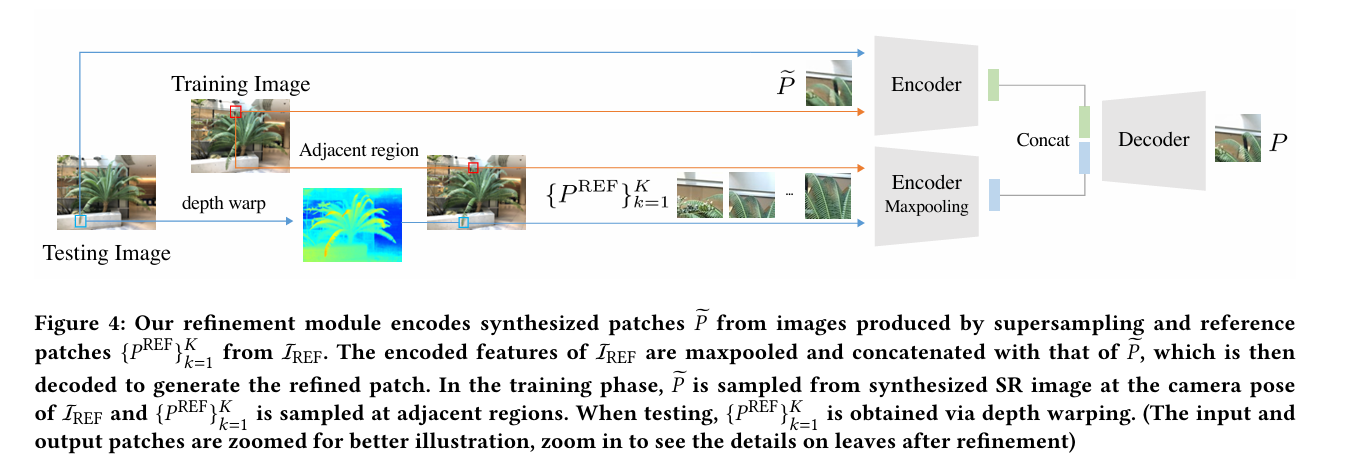
训练和测试时一些patch细节,暂且略过)(测试好像需要扭曲SR图像来对应reference)
2.3 experiments
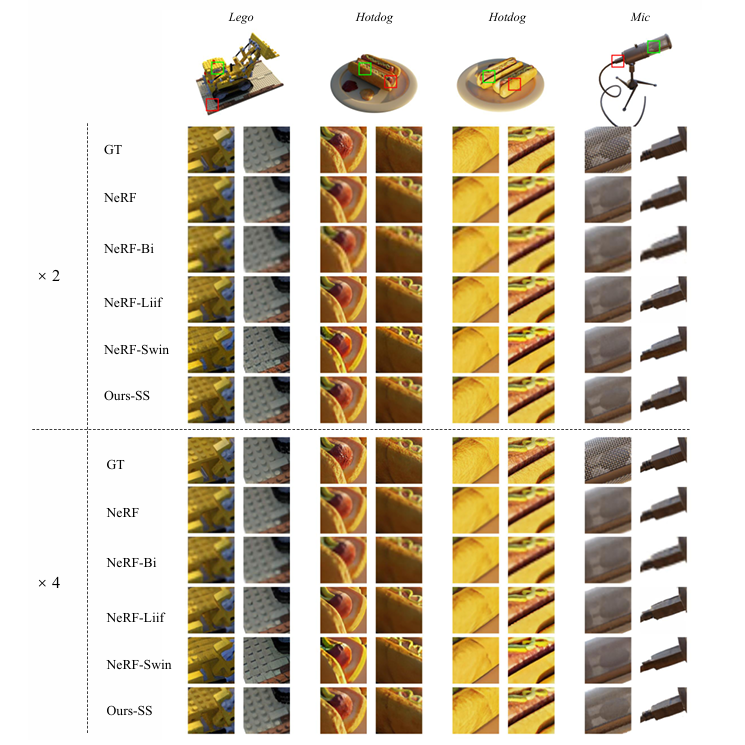
还是小小锐评一下,感觉NeRF-SR这个工作好像更多就是借用了渲染数据的增加(亚像素)来提升了分辨率,在理论上似乎没有特别值得mark的insight (? qwq 欢迎comment讨论
3 DiSR-NeRF
该论文介绍了一种名为 DiSR-NeRF 的扩散引导框架,用于视图一致的超分辨率 NeRF(神经辐射场)。其核心创新点在于利用强大的2D超分辨率模型,而无需依赖于高分辨率参考图像。该方法解决了低分辨率图像在不同视角之间存在的不一致性,通过引入迭代 3D 同步 (I3DS) 的策略,利用 NeRF 的多视图一致性特性,改善图像质量。
3.1 I3DS:Iterative 3D Synchronization
I3DS 分为两个阶段:上采样阶段和同步阶段。在上采样阶段,来自低分辨率 NeRF 渲染的图像通过扩散模型进行放大;在同步阶段,这些经过上采样的图像则用于更新3D表示。该过程交替进行,以引导模型收敛到一致的细节。
具体而言,在上采样阶段,首先对低分辨率图像进行4倍的放大。然后,通过标准的 NeRF 训练程序更新 NeRF 参数,同时进行多视图采样。这样的话,某个视图的细节信息能够在所有视角中得以统一。
3.2 RSD:Renoised Score Distillation
RSD 是一种本文提出的一种新的分数蒸馏目标,旨在结合使用祖先采样和评分蒸馏采样(SDS)的取长补短。RSD 通过优化过程中的中间去噪潜变量,逐步生成高分辨率图像。该过程通过一个线性递减的时间调度展开,逐步构建细节。 一方面,RSD 能够生成更锋利的细节;另一方面,它也能够保持与条件低分辨率图像的一致性。通过这种方式,RSD在各种细节方面都能显著提高性能,相较于传统的祖先采样法更具优势。


Comments